Morse Introduction

Morse Introduction
Jing OuyangTo describe Morse function with its usage in Spectral
首先感谢富卫师兄,还有郑老师,能让我接手这么大的一项网格工程。从代码进度来看,网格生成的基本流程已经走通了,但是在划分的时候省略了部分细节导致凹四边形出现。目前来看四边形网格生成技术已经相对成熟,接下来留给我的也只是一些基本的优化了。
系统结构
输入:三角网格
输出:四边形网格
中间值:Morse复型,四边形的网格块
简要概述一下对Morse方法的理解
Morse函数是定义在流形表面的一个标量场,这个标量场需要一定程度上表示出原拓扑结构的几何性质,最为常见的一组标量场是由 Laplacian 矩阵的首特征向量构造的。关于 Laplacian 矩阵,在曲面配准的工作记录中已经相对详细的描述了。但是, Morse 函数是一个很大的课题,有些学校甚至专门开一门课专门介绍这样的函数。但在四边形网格生成的工作里,只需要理解成 Laplacian Eigenfunctions 即可。
四边形网格生成技术的难点
什么样的曲面好进行四边形网格重构呢?最理想的肯定是一块四四方方的面块。但在工程上显然不会有这么理想的结构让我们处理,但很多流形都是这么变化过来的。什么样的变化是我们可以接受的呢?弯折一下,扭曲一下,这些都是可以接受的。但如果对面块进行拼接,甚至在上面挖个洞,这样就无法重构网格了。这就是因为这些操作会导致出现奇异点,理想的四边形网格结构上奇异点对应的 Vertex 可能不像其他点一样发出四条边,可能多一点也可能少一点。如何处理好这些奇异点是四边形网格生成需要克服的最大难点。
Critical Point
2006年这篇文章把重心放在在 Morse 函数里的鞍点,极大值点,极小值点上。这些点被命名为 Critical Point 。从某种意义上这些点在拓扑层面覆盖了奇异点,针对这些点进行划分即可规避四边形网格生成中不想遇到的东西。
Morse Complex
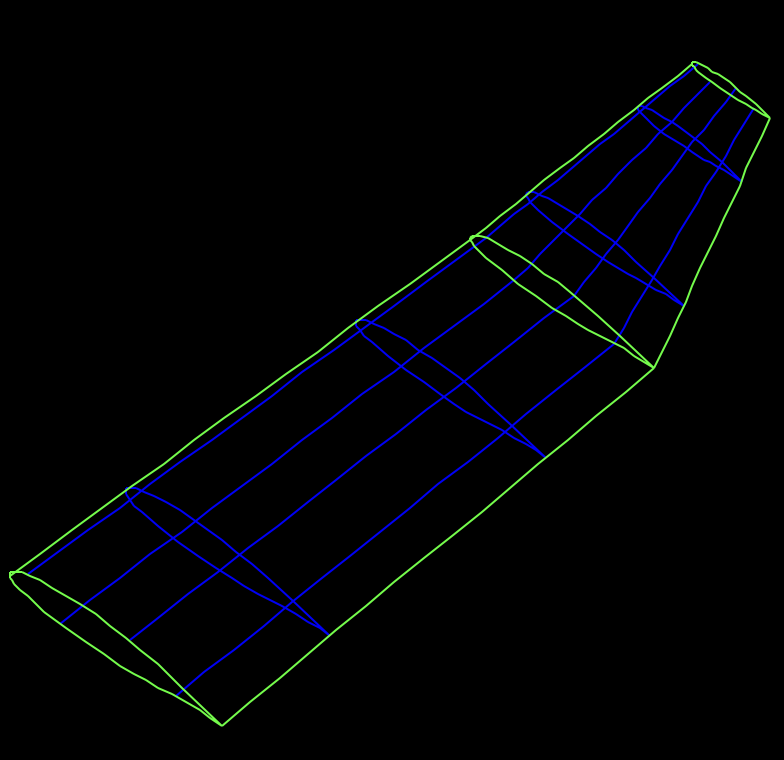
从鞍点出发,连接与之最近的一组极值点,这条线被定义为 Steep Line 。将所有的 Critical Point 和 Steep Line 整合到一个数据结构里,就是所谓的 Morse Complex 。这样的结构可以划分原有模型成若干个面片,针对这些面片分别进行同等速率的点采样和划分即可构建四边形网格结构。
一些技术上的难点
整体的理论思路比较简单,但四边形网格生成的难点更多在于一些工程上的细节。这也是接下来需要修正的内容
Critical point去噪
很多情况下鞍点和极大值极小值可能发生不匹配的现象,最终导致一些凹四边形的出现,严重影响网格质量。原文有介绍一组利用拉普拉斯特征值去噪的方法,但这样的去燥更多依靠的是人工经验。可以考虑引用曲面配准技术里的 feather point 优化,即利用其他特征向量的等值区域构建一个简化的线框(正如本文封面所示),原则上这些点集包含了原曲面的大量特征,那么 Critical Point 应该也包含在内,这样的思路可能之后需要实验来证实。
Steep line 光滑
这一步在原文有讲过,通过对构建出的 MS complex 映射到直角坐标上,利用二次线性规划的思路优化这个映射即可。目前代码采用测地线的方法计算最短路径,起到了光滑直线的作用但是很慢,还没法保留矩形特征。
下一步工作
结合已完成的工作,接下来将会针对未实现的难点进一步实现与优化,探索一些技术上的创新点。†
参考文献
- Shen Dong, Peer-Timo Bremer, Michael Garland, Valerio Pascucci, and John C. Hart. 2006. Spectral Surface Quadrangulation. ACM Trans. Graph. 25, 3 (2006), 1057–1066.
- Jin H , Zhang M , Jin M , et al. Spectral quadrangulation with orientation and alignment control[J]. Acm Transactions on Graphics, 2008, 27(5):147.
- MuyangZhang, JinHuang, XinguoLiu, and HujunBao. 2010.A Wave-based Anisotropic Quadrangulation Method. ACM Trans. Graph. 29, 4, Article 118 (2010).
- Ling R , Huang J , Juettler B , et al. Spectral Quadrangulation with Feature Curve Alignment and Element Size Control[J]. ACM Transactions on Graphics, 2015, 34(1):11.1-11.11.
- Fang X , Bao H , Tong Y , et al. Quadrangulation through Morse-Parameterization Hybridization[J]. ACM Transactions on Graphics, 2018, 37(4CD):1-15.