柱面和椭球面的识别策略

需求分析

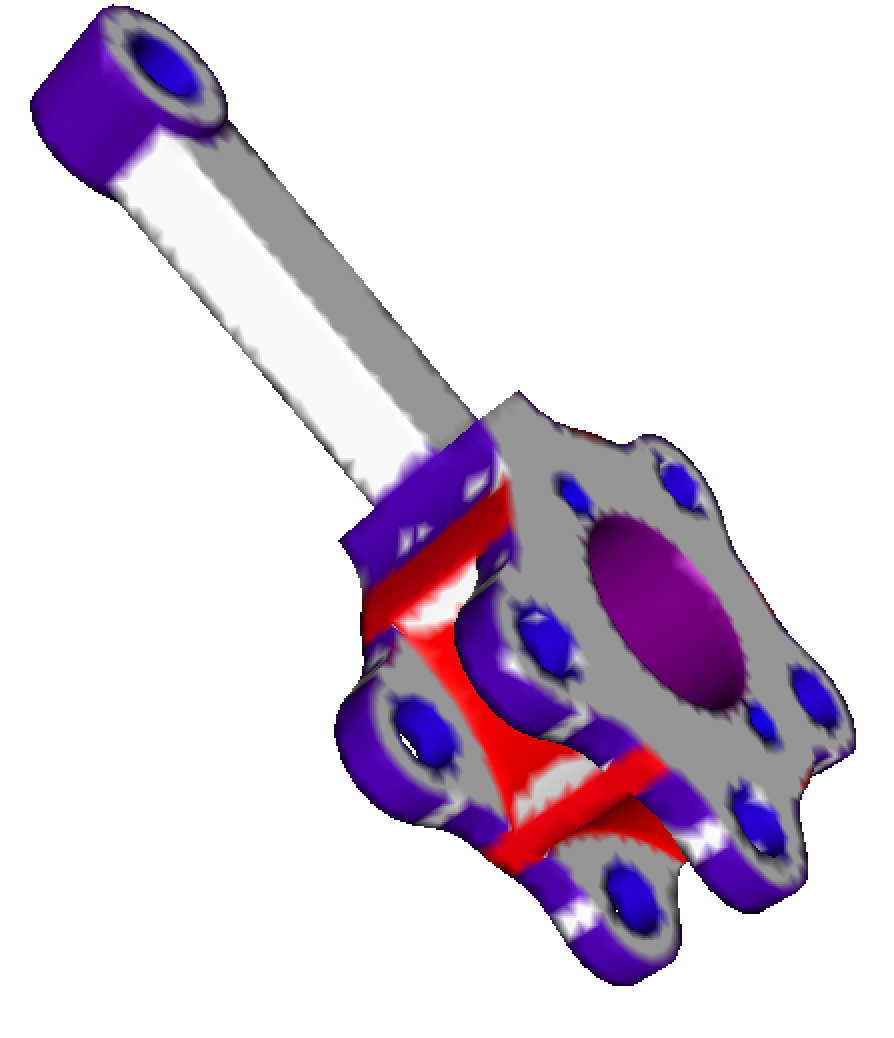
柱面往往在 CAD 领域用来表示倒角，其识别工作具有具有一定的意义。甲方提的需求对指定的模型生成六面体网格，针对模型局部地区参数的获取是至关重要的。在这个过程中，我们需要识别出柱面和椭球面。

还有一个更主要的原因是椭球识别是四月份写的，当时没记录，然后最近有了柱面的识别需求，再打开当时自己写的源码发现完全看不懂了😭，所以记录很重要。

输入输出

• 输入：局部可能包含柱面和椭球面的三维离散化网格
• 输出：柱面和椭球面的参数

识别策略

柱面和椭球面是相对比较好识别的，这是因为它们分别在线性代数的二次型中有明确的线性表现，通过旋转和平移可以将其转化为标准形式。根据转换后的二次型表现形式可以判断出是椭球柱面还是平面。

平移量获取

椭球面和柱面的识别都需要获取平移量，这个平移量是通过二次型的中心来获取的。对于二次型

$$
Ax^2 + By^2 + Cz^2 + 2Dxy + 2Exz + 2Fyz + 2Gx + 2Hy + 2Iz + J = 0
$$

其中心为 $(-G,-H,-I)$。将$(-G,-H,-I)$作为平移量代进来的话，二次型就变成了

$$a(x+G)^2 + b(y+H)^2 + c(z+I)^2 + d = 0
$$

看起来非线性好复杂，但是仅仅观察平移量的话，很神奇地就变成了线性的。

椭球面

椭球面的二次型表现形式为

$$
a(x+G)^2 + b(y+H)^2 + c(z+I)^2 + d = 0
$$

其中 $a,b,c$ 为正数，$d$ 为负数。椭球面的识别策略是通过 $a,b,c$ 的大小关系来判断的，如果 $a=b=c$，那么就是一个球面，如果 $a=b\neq c$，那么就是一个椭球面。

首先我们要确定什么是已知的，即$x,y,z$的值是输入，通过求解线性方程组即可得到不同维度下$x,y,z$的系数值，这些系数分别可通过对方程转化得到。其化简结果为

$$
a x^2 + 2 a G x + a G^2 + b y^2 + 2 b H y + b H^2 + c z^2 + 2 c I z + c I^2 + d = 0
$$

可以看到这是一个线性方程,我们暴力一点，直接将每个单项式的系数作为未知量代入10个点构建10个方程求出来即可。

不难看到的是 $x^2$ 的系数与 $x$ 的系数之间只差了一个 $G$，这样的话我们可以通过求解线性方程组来得到 $G$ 的值。同理，中心点的三个坐标值也可以通过这种方式求得。

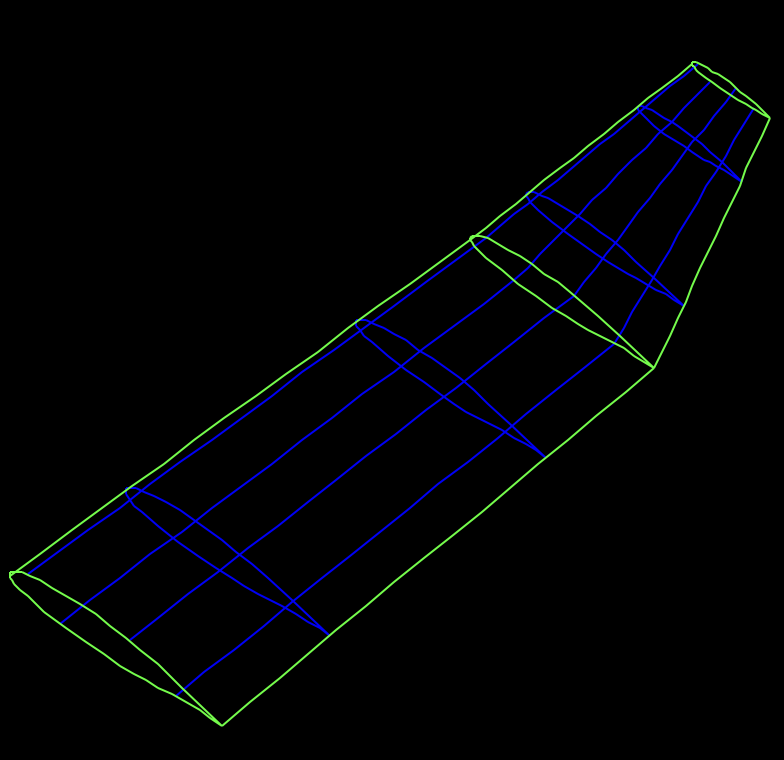
柱面

柱面的中心点和椭球面一样，通过平移量来获取，和椭球面不同的是，柱面的中心点是在柱面的轴上的，也就是说柱面的中心具有一个自由量，处理时默认为 $0$ 即可。柱面的中心也就成为了$(0,-H,-I)$。

其余步骤和椭球面一样，通过线性方程组求解即可。

旋转量获取

平移处理完那就是考研数学一倒数第二道大题的内容了，解特征值特征向量，求正交矩阵，化成标准形式，然后判断即可。

缺点与改进

为什么说这样的方法不鲁棒呢，因为算法的效果大幅度依赖于点的分布，尤其是局部点的判断，为保证效果不得不使用 BFS 取点，这样的点大概率会有在同一经纬线上的情况，导致方程解的扰动很大，目前可以想到的改进策略还的是找棱边，把圆形的棱边找到，然后将联通的棱边分开后判断是否为圆形并根据圆形的属性配对实现柱面分隔😢.