基于棱线配对的柱面识别策略

Jing Ouyang2024-07-052024-09-18

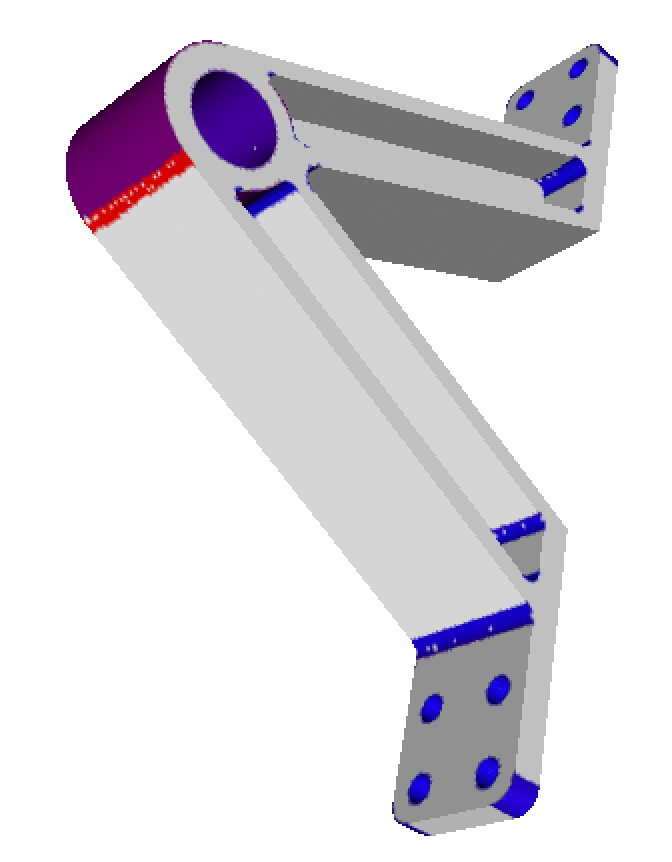
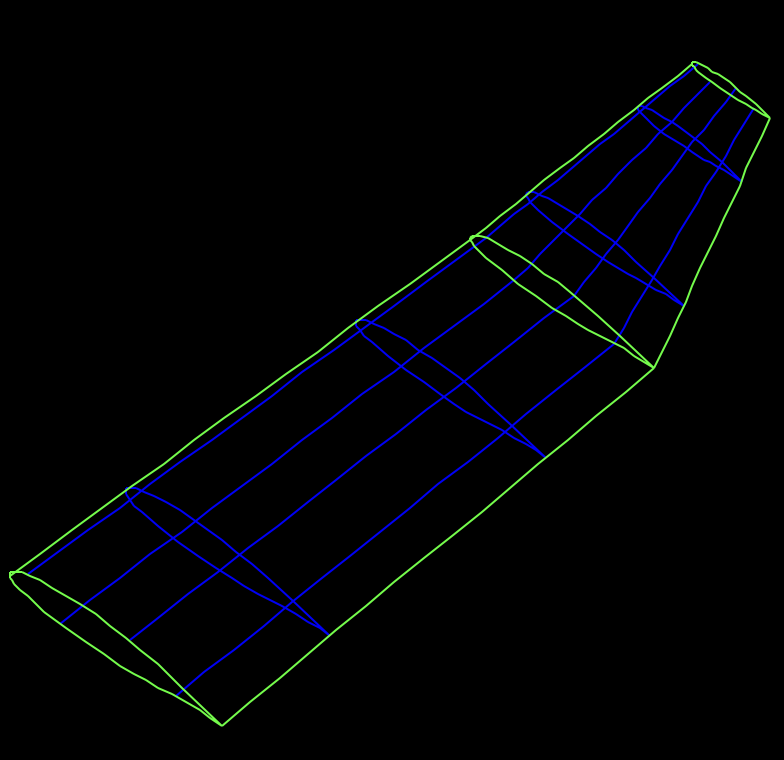
需求分析

为解决基于特征值特征向量的柱面识别策略不鲁棒的问题，本文在上周工作的基础上提出了一种基于棱线配对的柱面识别策略。

输入输出

输入：局部可能包含柱面和椭球面的三维离散化网格
输出：柱面的参数

识别策略

既然是基于棱线配对的柱面识别策略，那么首先我们需要获取棱线。在网格生成中，棱线是一个很重要的概念，它是由两个顶点组成的线段，而顶点是由三角形面共享的。因此，我们可以通过遍历所有的三角形面，获取所有的棱线。在此之后，需要对棱线进行几何意义上的分段与拟合，获取棱线局部的曲率半径及曲率中心，选择出属于局部圆形的棱线。在此之后，需要对识别出的圆进行剪枝，这一步比较依赖于经验，因为不同模型数量级和大小不同，剪枝策略下对应的阈值参数也不同。最后需要对剪枝后的圆进行参数化，并将各个圆形两两配对，得到最终的柱面参数。

棱线获取

设置宏定义`EDGE_INDEX’，通过遍历所有的边，根据其相邻面片法向量的差是否大于’EDGE_INDEX’来判断是否为棱线。

以下是一个代码示例，并非基于MeshLib的实现，仅供参考。

#define EDGE_INDEX 0.8

for (int i = 0; i < mesh->numEdges(); i++) {
    Edge *edge = mesh->edge(i);
    if (edge->isBoundary()) continue;
    Face *face1 = edge->halfedge(0)->face();
    Face *face2 = edge->halfedge(1)->face();
    if (face1 == NULL || face2 == NULL) continue;
    Vector3d normal1 = face1->normal();
    Vector3d normal2 = face2->normal();
    if (normal1.dot(normal2) < EDGE_INDEX) {
        edge->isEdgeLine = true;
    }
}

棱线拟合

对于识别出的棱线，我们需要对其进行拟合，获取其曲率半径及曲率中心,由于三点定圆,所以选择棱线上相互连续的三个点进行拟合,比较建议的选点策略是深度优先选择，可以尽可能的减少三点不共面的情况，三点不共面的情况会有但是实际上几乎不会影响到结果,毕竟很难找到对应的圆来与之配对。

以下是一个代码示例，并非基于MeshLib的实现，仅供参考。

for (int i = 0; i < mesh->numEdges(); i++) {
    Edge *edge = mesh->edge(i);
    if (!edge->isEdgeLine) continue;
    Vertex *v1 = edge->halfedge(0)->vertex();
    Vertex *v2 = edge->halfedge(1)->vertex();
    Vertex *v3 = edge->halfedge(0)->next()->vertex();
    Vector3d p1 = v1->position();
    Vector3d p2 = v2->position();
    Vector3d p3 = v3->position();
    Vector3d n1 = v1->normal();
    Vector3d n2 = v2->normal();
    Vector3d n3 = v3->normal();
    Vector3d center = getCircleCenter(p1, p2, p3);
    double radius = (p1 - center).norm();
    edge->circleCenter = center;
    edge->circleRadius = radius;
}

棱线剪枝

异常圆的剔除

剪枝主要去除的是棱线度不为2的点和半径过大的点，应该很好操作，这里不再赘述。

相近圆的合并

对于相近的圆，我们需要将其合并，这里的相近是指圆心距离小于一定阈值的圆，这个阈值是需要根据实际情况调整的，可以重载operator==来实现。

struct circle
{
    double radius;
    CPoint center;
    CPoint normal;
    
    bool operator== (const circle& c) {
        return abs(radius - c.radius) < ZERO && ((center - c.center).norm() < ZERO) && ((normal - c.normal).norm() < ZERO);
    }
    
    circle(double r,CPoint c,CPoint n):radius(r),center(c),normal(n){}
};

棱线配对

对于剪枝后的圆，我们需要将其两两配对，得到最终的柱面参数。


void CirclePairRe<M>::getCirclePair()
    {

        for(int i = 0 ; i < circlelist.size() ; i++)
        {
            // if(circleIndex[i] < 2) continue;
            for(int j = i ; j < circlelist.size() ; j++)
            {
                // if(circleIndex[j] < 2) continue;
                if(abs(circlelist[i].radius - circlelist[j].radius) <ZERO && (circlelist[i].normal ^ circlelist[j].normal).norm() < ZERO && ((circlelist[i].center - circlelist[j].center)^circlelist[i].normal).norm() < ZERO ) 
                {
                    auto cylinderCenter = (circlelist[i].center + circlelist[j].center) / 2;
                    auto cylinderHeight = (circlelist[i].center - circlelist[j].center).norm();
                    if(cylinderHeight < ZERO) continue;
                    auto cylinderRadius = circlelist[i].radius;
                    auto centerline = (circlelist[i].center - circlelist[j].center);
                    centerline /= centerline.norm();
                    auto rotate = new Eigen::Matrix3d();
                    CPoint x(-centerline[1], centerline[0], 0);
                    x /= x.norm();
                    CPoint y = centerline ^ x;
                    *rotate << x[0], x[1], x[2],
                               y[0], y[1], y[2],
                               centerline[0], centerline[1], centerline[2];
                    cylinder *cc = new cylinder(cylinderRadius,cylinderHeight,cylinderCenter,rotate);
                    cylinderlist.push_back(*cc);
                }
            }

        }
    }