论文阅读:Stochastic Computation of Barycentric Coordinates
论文阅读:Stochastic Computation of Barycentric Coordinates
Jing Ouyang背景
重心坐标在三维动画制作中可以被当作几何形变的启发,从而获得一系列应用,本文是最新的重心坐标计算方法,利用大量前置知识获得一个不依赖于控制点数量以及质量的重心计算方法,高效地获得控制点以及三维物体本身的映射关系。
本文不仅仅是对 《Stochastic Computation of Barycentric Coordinates》的阅读笔记,还是对几何形变控制相关工作的阅读总结,会介绍一系列经典的重心坐标计算方法以及他们的应用。
插值算法(光栅化)
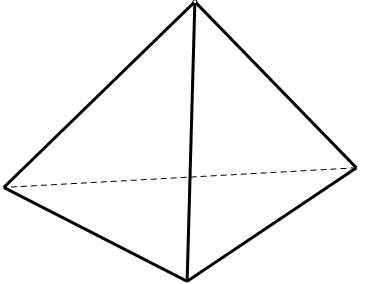
在计算机图形学中,插值算法是一种用于计算两个已知数值之间的中间值的方法,通常用于计算两个已知颜色之间的中间颜色,或者计算两个已知点之间的中间点。插值算法的应用非常广泛,例如在图像处理中,插值算法可以用于图像的缩放、旋转、变形等操作。比较常见的插值算法应用是三角网格面片着色的插值算法,通过定义各个点的颜色即可实现面片着色。除此之外还包括纹理贴图和法向贴图等应用方法,理论上针对一个三角形,任何三维及以上的指标都可以通过定义三角形上三个点的指标来获取三角形内部任意一点的指标,点的坐标也不例外。
目标(输入输出)
框架(Cage)内部任意一点坐标信息的 Deformarion 。
- 输入:三角形的三个顶点坐标,以及三个顶点的指标值。
- 输出:三角形内部连续空间上任意一点的指标值。
Compute Coordinates
- 三角形的三个顶点坐标:$A,B,C$
- 三个顶点的指标值:$a,b,c$
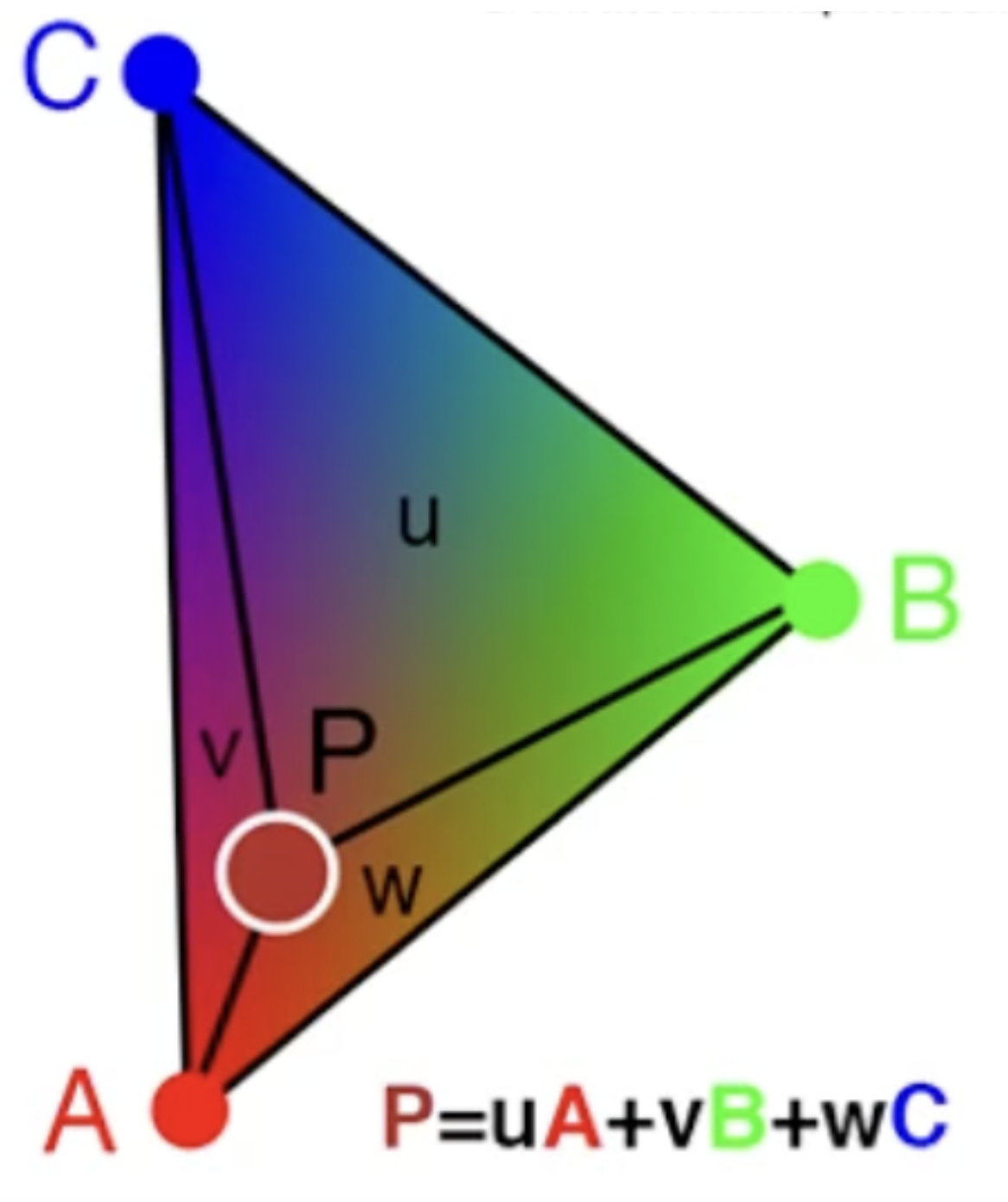
对于三角形内部任意一点 $P$,可以通过以下公式计算其指标值:
$$
P = aA + bB + cC
$$
其中
$$
a + b + c = 1
$$
通常而言,指标值 $a,b,c$ 在三角形单形内部可以通过其对应顶点对边所在的子三角形的面积比例来计算。
$$
a = \frac{S_{BCP}}{S_{ABC}}
$$
$$
b = \frac{S_{ACP}}{S_{ABC}}
$$
$$
c = \frac{S_{ABP}}{S_{ABC}}
$$
形变表示
获取到三角形内部任意一点从三角形各个顶点的映射关系$F(P,A,B,C) = 0$后,可以通过该映射来通过控制三角形来控制三维物体的形变。
$$
F(P,A,B,C) = F(P’,A’,B’,C’)
$$
其中 $P’$ 为形变后的点,$A’,B’,C’$ 为形变后的三角形顶点。
Mean Value Coordinates
利用插值的方法可以实现简单形变,但这仅限于 Cage 是单型的情况,如果要对复杂模型进行基于物理的规律性运动,就需要定义更为复杂的 Cage,而针对复杂的 Cage 要实现插值映射就需要 Mean Value Coordinates(MVC) 的方法。
目标(输入输出)
输入
- Cage (可以是凸的复形)
- 位于 Cage 内部的任意一点坐标(或者不超越 Cage 的形状集合)
输出
框架(Cage)内部任意一点坐标信息的 Deformarion 映射。
Compute Coordinates (以二维为例)
作为一个比较通用也没有那么困难的算法,网上已经有很多关于 MVC 的介绍,证明思路也多种多样,本篇也是对其中一篇的搬运。
MVC 同样是计算重心坐标,针对凸多面体点分布不均匀的状况综合计算,通过计算每个顶点到目标点的角度来计算其重心坐标。
- 多边形的顶点坐标:$P_1,P_2,P_3,…,P_n$
- 多边形的顶点的指标值:$a_1,a_2,a_3,…,a_n$
- 目标点坐标:$v$
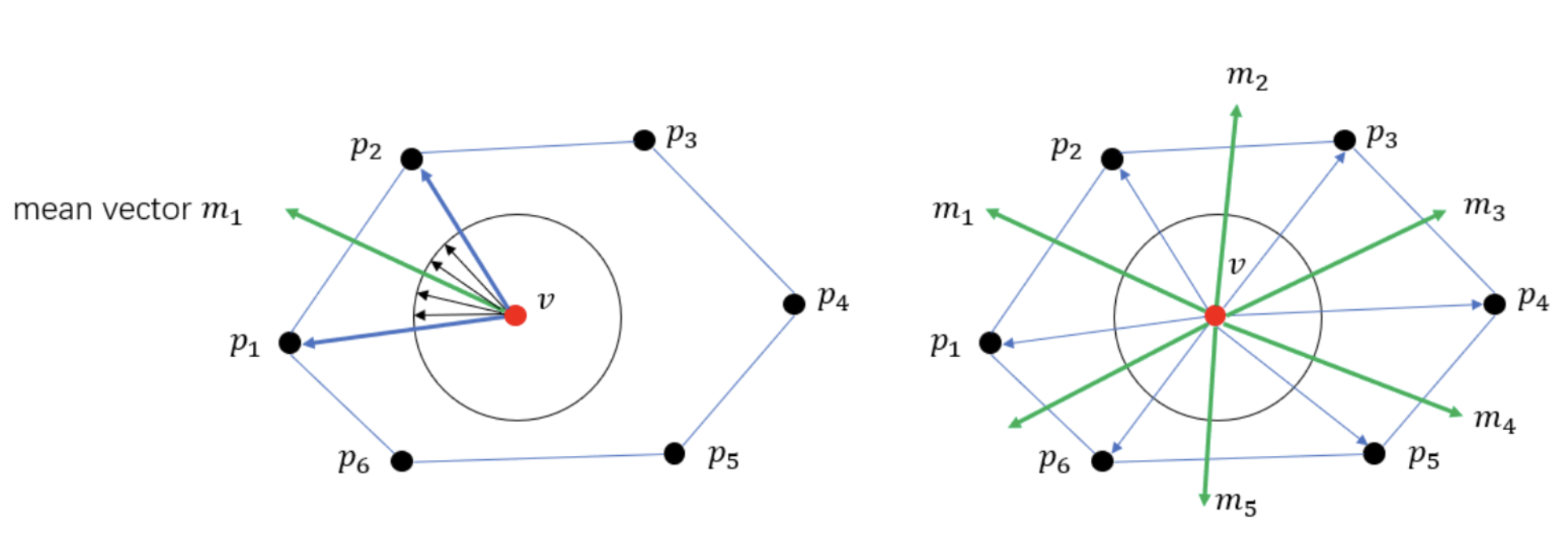
如图所示,在二维空间上的多边形内部重心 $v$ 以其为圆心构建一个单位圆后将 Cage 上的点映射到单位圆上,两两一组构建其均值向量 $m_i$ ,根据重心定义各个均值向量的和应当为 0 。
$$
\sum_{i=1}^{n} m_i = 0
$$
$m_i$ 的几何意义是这一段圆弧上所有单位向量的积分,与这段圆弧对应的边长有关。由此得出 $m_i$ 的计算公式:
$$
m_i = \tan[\frac{\alpha_i}{2}] \cdot (\frac{v P_{i+1}}{||v P_{i+1}||} + \frac{v P_i}{||v P_i||})
$$
其中 $\alpha_i$ 为 $v p_{i+1}$ 与 $v P_i$ 之间的夹角。
不妨定义 $m_i$ 之前的系数为 $\lambda_i^1$ 和 $\lambda_i^2$ ,则有:
$$
\lambda_i^1 = \frac{\tan[\frac{\alpha_i}{2}]}{||v P_{i+1}||}
$$
$$
\lambda_i^2 = \frac{\tan[\frac{\alpha_i}{2}]}{||v P_i||}
$$
且有
$$
m_i = \lambda_i^1 \cdot v P_{i+1} + \lambda_i^2 \cdot v P_i
$$
$$\sum_{i=1}^{n} m_i = 0$$
故
$$
(\lambda_1^1 + \lambda_n^2) \cdot v P_1 + (\lambda_2^1 + \lambda_1^2) \cdot v P_2 + … + (\lambda_n^1 + \lambda_{n-1}^2) \cdot v P_n = 0
$$
由此可知 $v P_i$ 的系数 $k_i$ 为 $\lambda_i^1 + \lambda_{i-1}^2$
$k_i$ 单位化后即可获得以 $v$ 为重心时各点的权重 $w_i$。
result
因此可以获得通用的插值公式对应的权重
$$
w_i = \tan(\frac{\alpha_i}{2}) \cdot \frac{1}{||v P_{i+1}||} + \tan(\frac{\alpha_{i-1}}{2}) \cdot \frac{1}{||v P_i||}
$$
Harmonic Coordinates
MVC 是一种比较通用的插值算法,但是其计算量较大,而且对于非凸的 Cage 也无法很好的计算,因此有了 Harmonic Coordinates 的方法。
根据笔者的理解,Harmonic Coordinates (HC)其基本思想是通过模拟物体的弹性形变来计算其重心坐标,相比起 MVC 而言 HC 主要在于添加了两条新的限制,一是在控制点无负值的情况下内部同样无负值,二是插值函数在 Cage 内无极值,正是因为后者无极值的限制来自于 Harmonic 函数的特性,因此得名 Harmonic Coordinates。
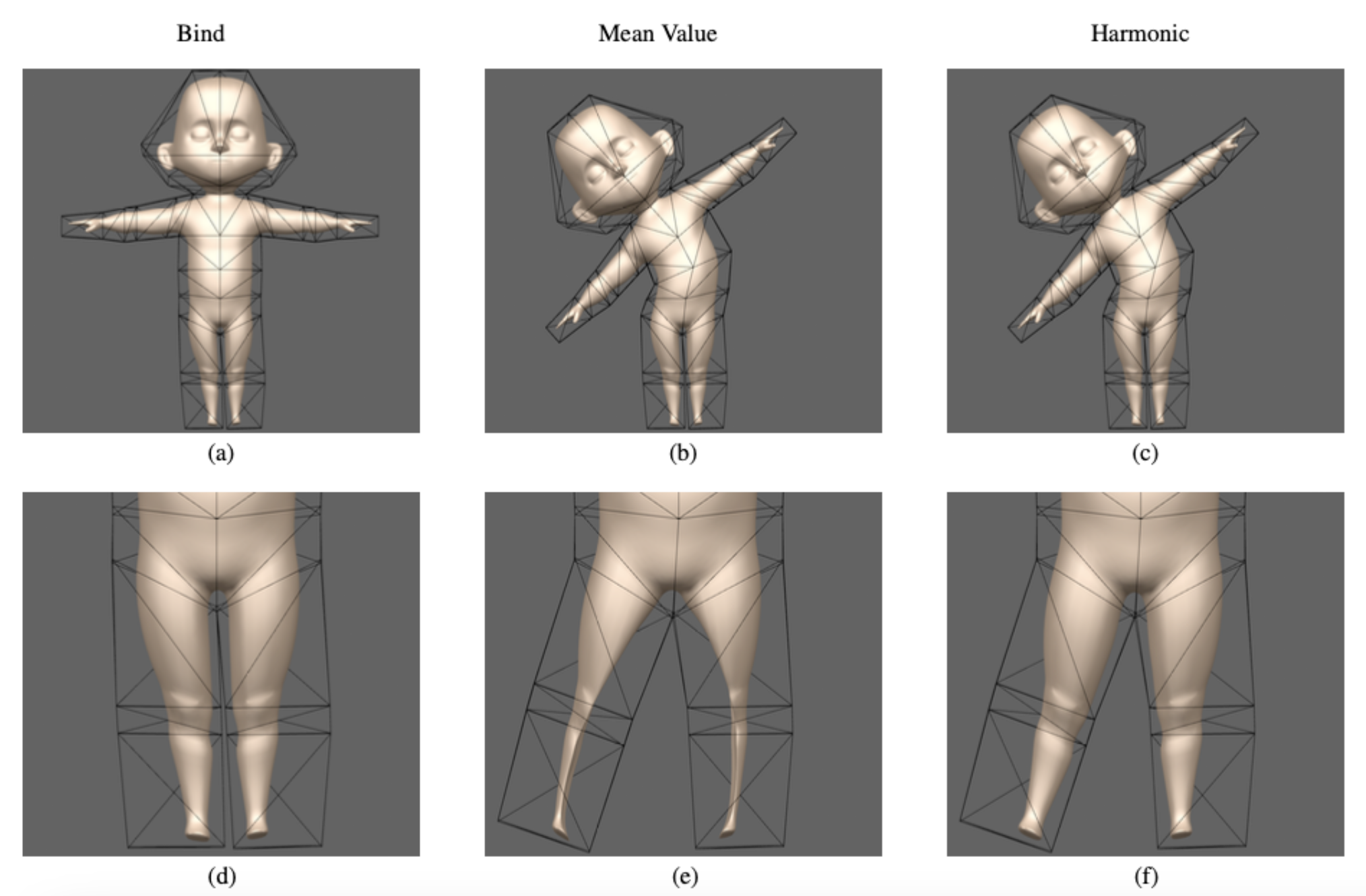
该图表示了 MVC 的一大缺陷,在非凸的 Cage 上计算的重心坐标会出现负值,因此在对人物张开双腿的动作时会导致人物的腿部形变不自然,而 HC 则可以很好的解决这一问题。
调和坐标的计算方法与 MVC 类似,但是在计算均值向量时添加了一个限制条件,即均值向量的和为 0,这样可以保证在 Cage 内部的任意一点的重心坐标都是正值,若因为该条件无法保证最后的线性方程组有解,则可以通过对 Cage 的划分来保证其有解,对不同的 Cage 分别处理后为避免翻转或者自相交,会引入 Maya 的有关模块来平滑化保证其不会出现翻转。
Reproducing Kernel Particle Methods(PKPM)
PKPM 是一种基于粒子的插值算法,个人感觉和最小二乘法差不多,其本质也是为消除内部极值点,其基本思想是定义一个 Reproducing Kernel Function 来表示 Cage 内部一点到 Cage 上各点的映射关系,是距离公式的优化,可以使得 Cage 的形状不会影响到内部的形变,但这样会导致 Harmonic Coordinates 的相关属性丢失而丧失调和性,因此使用 RKPM 来使得该映射重获调和性。
- 定义一个 Reproducing Kernel Function $K(x,y)$
根据 $K(x,y)$ 获得 Cage 上一点 $y$ 到内部一点 $x$ 的映射关系 $\phi(y)$
- 定义一个 $u(x)$ 来线性表示 $x$ 的映射关系
$$
u_v(x) = \arg \min_{u} \int_C k(x,y) ||u^t(y) - \phi(y)||^2 dy
$$
其中 $C$ 为 Cage
- 离散化计算积分
$$
u_v(x) = \arg \min_{u} \sum_{k} w_k ||u^t(y_k) - \phi(y_k)||^2
$$
其中 $w_k$ 为通过 $K(x,y)$ 离散化得出的权重
计算出 $u(x)$ 后即可获得 Cage 内部任意一点的线性映射关系,去除 Kernel 带来的高频噪声。
Stochastic Computation of Barycentric Coordinates
在收获前置知识后,这篇文章基本就是对各方法的应用,这里凭笔者本人理解简单过一遍思路。
输入
- 一个 Cage $C$,其上有 $n$ 个顶点 $P_1,P_2,…,P_n$ 被称作控制点
- 一个目标点 $v$
输出
- 目标点 $v$ 在 Cage $C$ 上的重心坐标 $w_1,w_2,…,w_n$
方法
- 对每个控制点添加一个标量 $g_v$ ,个人感觉是为摆脱 $\phi$ 和为 1 的限制。
由此可以获得 Cage 上连续空间里的任意一点 $y$ 的标量值
$$
g(y) = \sum_v \phi_v(y) g_v
$$
- 核函数 $K(x,y)$ 用于表示 $x$ 到 $y$ 的距离的映射,使得控制点的插值向 Cage 内部生长
$$
f(x) = \int_C K(x,y) g(y) dy
$$
- 将控制点的权重 $g_v$ 线性分离出来,其系数整理为 $\alpha_v(x)$
$$
f(x) = \sum_v \alpha_v(x) g_v
$$
$$
\alpha_v(x) = \int_C K(x,y) \phi_v(y) dy
$$
- 定义出 $u$ 来表示 $x$ 的线性映射
$$
u_v(x) = \arg \min_{u} \int_C K(x,y) ||u^t(y) - \phi(y)||^2 dy
$$
离散化:
$$
u_v(x) = \arg \min_{u} \sum_{k} w_k ||u^t(y_k) - \phi(y_k)||^2
$$
目标:
$$
\tilde(a_v(x)) = u_v(x)^t x
$$
- 求解
$$
u_v(x) = M^{-1} m_v(x)
$$
$$
M = \sum_{k} w_k y_k y_k^t
$$
$$
m_v(x) = \sum_{k} w_k y_k \phi_v(y_k)
$$
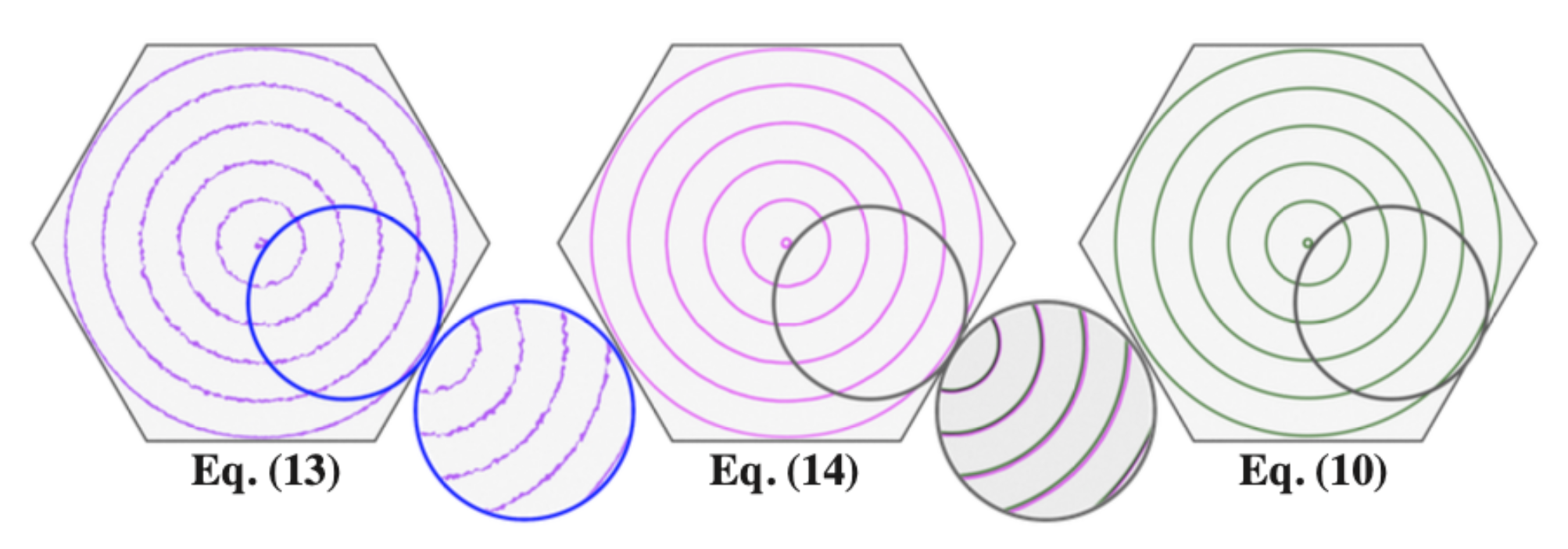
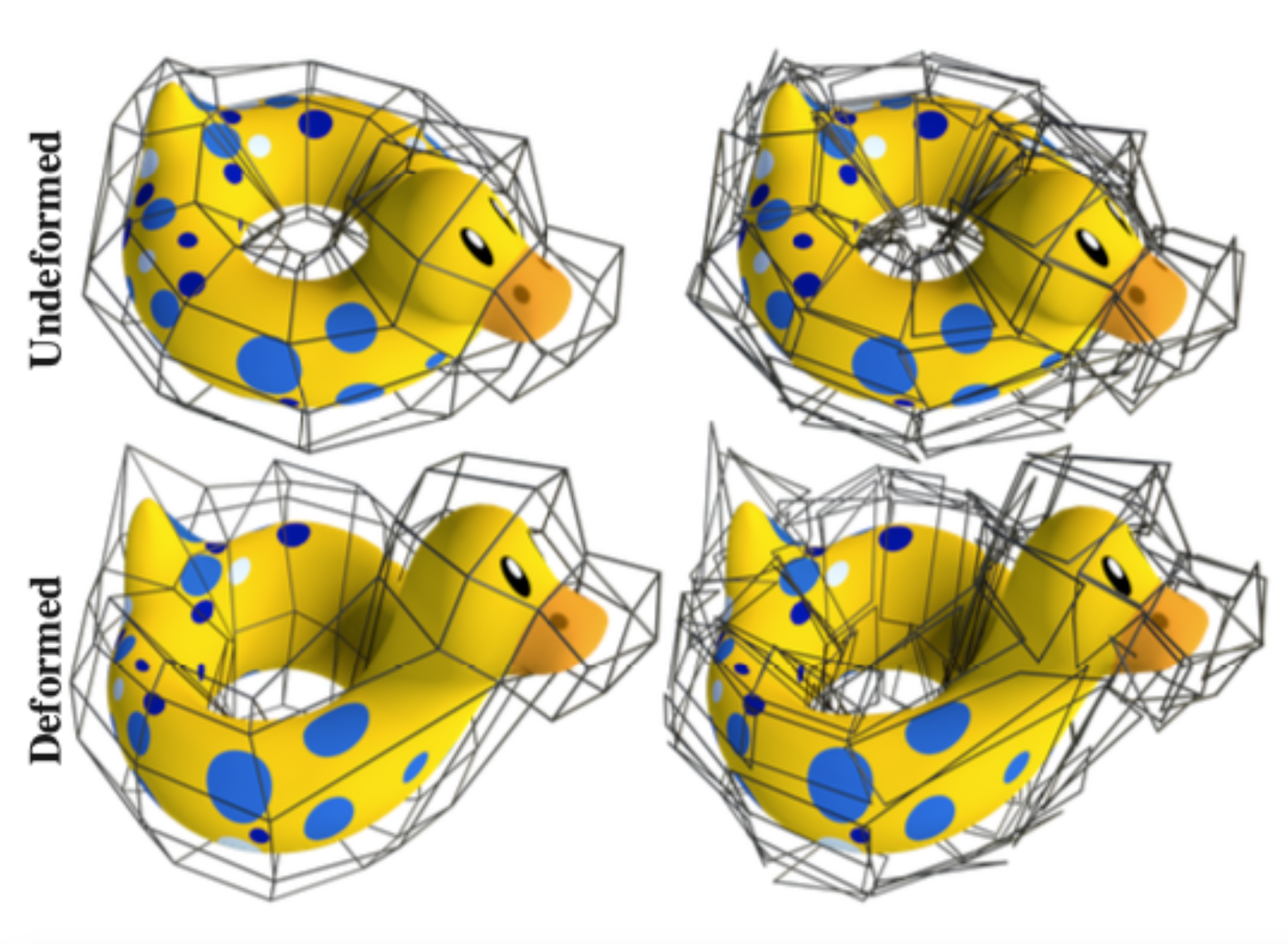
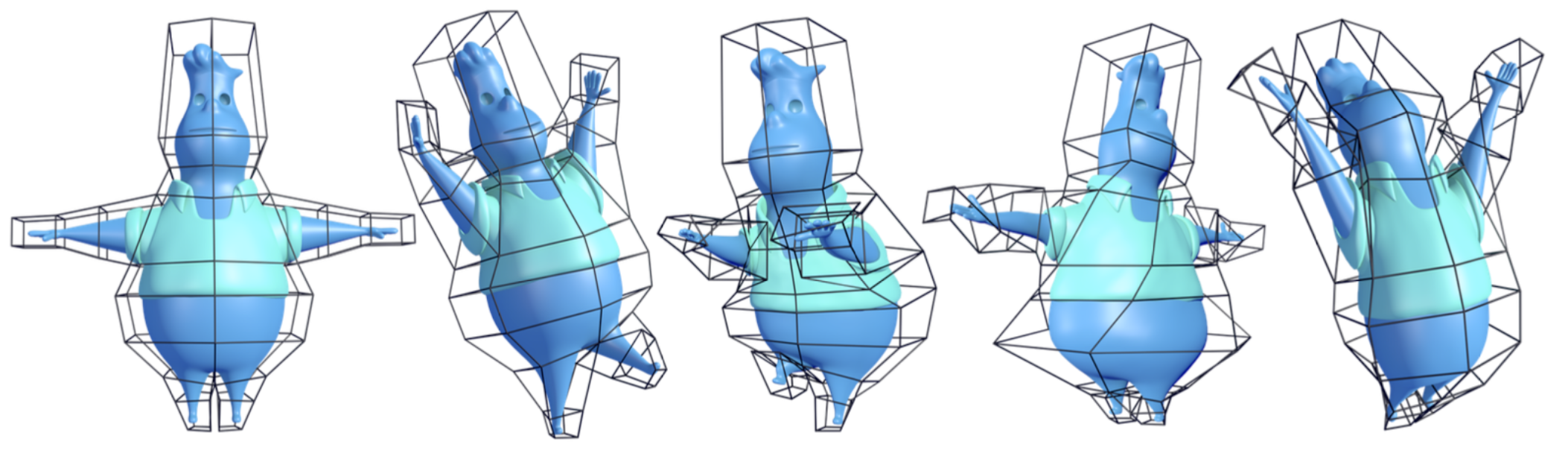
效果展示
本文还引入了去噪算法,使得最后的结果更加平滑,笔者精力有限就不再展开了,下图是一个相当典型的效果展示,可以看到在分布很差的 Cage 和分布很好的 Cage 上使用本文算法计算重心坐标进行形变的效果几乎一致