背景

曲面分块，尤其是二次曲面分块，在工业应用中尤为重要，不仅仅是物体扫描点云并且逆向构建 CAD 模型，还是工业设计中棱边和倒角的识别，以及工业机械零件的设计和制造，都起着至关重要的作用。本文将介绍一篇今年的 Transaction on Graphics ，来自深圳大学，题目是《Split-and-Fit Learning B-Reps via Structure-Aware Voronoi Partitioning》。这篇文章提出了一种新的曲面分块方法，巧妙运用 无符号距离场(UDF) 和 Voronoi 分割 的方法，运用了无符号距离场和表面曲率的关系，在空间上实现了场的分块，从而实现了曲面的 Split,唯一美中不足的是本文最后还是使用深度学习的方法计算场，虽然这有效避免了传统方法针对不同模型其曲率分块参数不同需要单独设置的问题，但是深度学习的方法对于工业应用的可解释性和泛化性还是有待考量，并且该文章在缺点分析出提出的分块效果不理想的情况，笔者认为这也可能是深度学习数据集不够或者模型结构还有优化空间导致的。

预备知识

无符号距离场(UDF)

无符号距离场是一种用于表示曲面的方法，其定义为：

$$
\text{UDF} = \min_{i} { | \mathbf{p} - \mathbf{p}_i | }
$$

其中 $\mathbf{p}$ 为曲面上的点，$\mathbf{p}_i$ 为曲面上的点集，即曲面上的点到点集的最小距离。无符号距离场的优点是可以用于表示曲面的局部特征，例如曲率，法向量等。

以之前给过的模型为例，给出无符号距离场的可视化结果：

Voronoi 分割

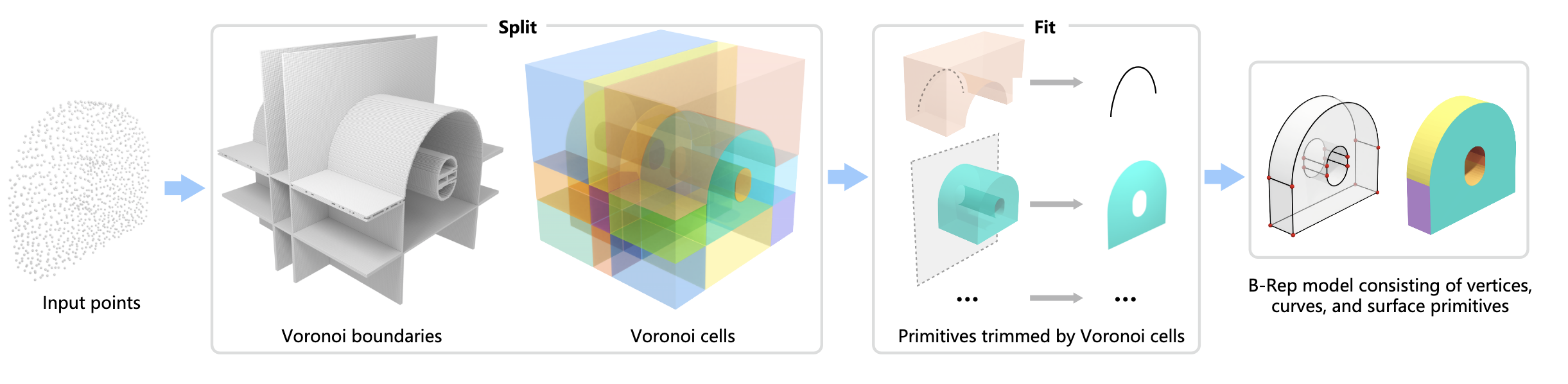
Voronoi 分割是一种用于将空间分割为不同区域的方法，通常的概念是三角形网格将点映射成面，而面被映射成点的网格对偶形式，而在这里的 Voronoi 分割是将空间分割为不同区域，将模型的边界映射成一个体元，因此可以用于曲面的分块，每个体元 (Cell) 表示一个曲面块。

引用文章中的配图，给出 Voronoi 分割的示意图:

B-rep 表示

B-rep 是 Boundary Representation 的缩写，是一种用于表示曲面的方法，其定义为：

$$
M = { (V, E, F, \partial , \mathcal{P}) }
$$

其中 $V$ 为顶点，$E$ 为边，$F$ 为面，$\partial$ 为边界或者点边面的拓扑连接关系，$\mathcal{P}$ 为参数化曲面。

Split-and-Fit

这篇文章核心方法在于 Split ,相对的在 Fit 阶段使用了较为传统的最小二乘法，通过相对更加优秀的 Split 来提高曲面分块拟合的效果。

本文 Pipeline 如下：

Split

这篇文章主要思路是利用无符号距离场和曲率的关系，通过无符号距离场的二阶导来表示曲率，从而实现曲面的分块。具体的方法是通过无符号距离场的二阶导数来表示曲率，然后通过曲率的变化来实现曲面的分块。

无符号距离场的二阶导的几何意义及局限性

但是这里有一个问题，无符号距离场的二阶导数是不稳定的，这篇文章图中所表示的场的信息如果是单纯的用差分表示导数的话是不会有这么好的效果的，因此需要计算局部特征值，即通过无符号距离场的梯度和 Hessian 矩阵来计算曲率。

Hessian 矩阵的定义为：

$$
H = \begin{bmatrix}
\frac{\partial^2 f}{\partial x^2} & \frac{\partial^2 f}{\partial x \partial y} & \frac{\partial^2 f}{\partial x \partial z} \cr
\frac{\partial^2 f}{\partial y \partial x} & \frac{\partial^2 f}{\partial y^2} & \frac{\partial^2 f}{\partial y \partial z} \cr
\frac{\partial^2 f}{\partial z \partial x} & \frac{\partial^2 f}{\partial z \partial y} & \frac{\partial^2 f}{\partial z^2}
\end{bmatrix}
$$

其中 $f$ 为无符号距离场，通过 Hessian 矩阵的特征值来计算曲率，其中最大特征值为最大曲率，最小特征值为最小曲率。

可以看出，对无符号距离场的三阶导即是 Voronoi 分割的的依据，看似巧妙简单，但实际上计算量巨大，不仅如此，要获得 Voronoi 轮廓是需要对三阶导计算等值面的，针对每个模型都需要重新计算，这是一个非常耗时的过程，本人利用 CUDA 加速复现了一些的 Voronoi 分割算法

为什么要用 CUDA 加速呢，因为 UDF 对噪声及其敏感，想要达到上面所现实的效果，需要接受千万级别的点云数据输入，否则会得到下图的噪声数据,这是 CPU 无法承受的，因此需要用 GPU 加速，这也说明了数理方法的鲁棒性是及其有限的。

基于深度学习的曲面分块

这篇文章介绍了这么多 UDF 的数理意义，但最后其实并没有使用 UDF 来计算曲面的分块，输入数据为 $R^3 *4$ 的UDF 数据，输出为 $R^3 * 1$ 的曲面分块数据，这里使用了深度学习的方法，通过卷积神经网络来计算曲面的分块，这里的深度学习方法是为了避免传统方法针对不同模型其曲率分块参数不同需要单独设置的问题。

至于深度学习的方法，这里就不展开了，是很传统的 UNet 结构，而且深度和参数仔细研究过感觉没有什么说法，这里就不展开了。

Fit

这里的 Fit 阶段使用了较为传统的最小二乘法，通过相对更加优秀的 Split 来提高曲面分块拟合的效果,并没有什么亮点，这里也不做赘述了。

最小二乘法

最小二乘法是一种用于求解线性方程组的方法，其定义为：

$$
\min_{\mathbf{x}} | A \mathbf{x} - \mathbf{b} |
$$

其中 $A$ 为系数矩阵，$\mathbf{x}$ 为未知数，$\mathbf{b}$ 为常数项。

这里的最小二乘法是用于拟合曲面的参数，通过曲面的参数来拟合曲面的分块。

一般情况的二次曲面需要求解三元二次参数,道理是一样的，计算所有的二次和一次项的参数即可。

Result

从文章结果看，效果肯定是独一档的，毕竟是一篇开源的 TOG 论文。

但由于是基于深度学习的 B-rep 分块方法，目前的开源算法还有提高空间，以开源代码给出的示例来看，分块后的二次曲面只做到了拓扑上连续而没有做到几何上的连续，这也是深度学习方法的局限性，并且根据笔者本人猜测，根据论文后面的 Future Work 目前部分模型还有分块不够水密的情况，在数理情况下这是很合理的，因为三阶导等值面计算错误，但深度学习会出现这样的问题，那很有可能是数据集不够理想导致，毕竟 Voronoi 图的手动标注本身就是很困难的，因此可以考虑设计出一套无监督的优化算法，使用高质量点云数据集来训练，这样可以提高模型的泛化性。

Related Work

在这篇文章之前还有很多点云或者曲面分块的工作，这里也不展开了，稍微提一下：

HPNet: Deep Primitive Segmentation Using Hybrid Representations ICCV 2021

这篇文章创新在根据连续性和光滑特征重构网格，根据多模态的信息指导了点云的分块。

ComplexGen: CAD Reconstruction by B-Rep Chain Complex Generation ACM Trans. Graph. 2022

这篇文章创新在于通过 B-Rep 链复杂生成，并引入注意力机制，重构 CAD 模型。

Surface and Edge Detection for Primitive Fitting of Point Clouds siggraph 2023

这篇文章利用 Sharp 边的属性来指导曲面分块，此外将Primitive Fitting 和 Sharp Edge Detection 结合，提高了曲面分块的效果。

总结

这篇文章是一篇很有意思的文章，能想到利用无符号距离场来指导曲面分块，这是一个很有创意的想法。也取得了很显著的效果，但优化空间还是存在的，重构的二次曲面不够水密甚至不包含统一的定向信息等小细节是可以优化完然后应用到工业上的，是相当有意义的一篇文章😋。